Программирование на MQL II. Поиск
Дата: 3.3.07 | Раздел: MQL программирование
Программирование на MQL II. ПоискПрограммирование на MQL II. Поиск
Уважаемые читатели, в Forex Magazine 2004 №6 в статье "Программирование на MQL II: Сортировка методом пузырька, продолжение" была допущена небольшая ошибка. Обратите внимание, что во время добавления новой переменной is_sorted изначально ей должно присваиваться значение "true", а не "false". Ошибка допущена только в описании кода, сам же код верен. Таким образом, исправленное предложение выглядит так: "Каждый раз, перед тем как в очередной раз перебирать и сравнивать элементы массива, будем присваивать этой переменной значение true. Если мы поменяем хоть раз значения элементов массива, то присвоим ей false."
В прошлых номерах мы рассмотрели сортировку методом пузырька (Forex Magazine 2004 №5 - №6, Программирование на MQL II: Сортировка методом пузырька). Теперь обсудим способы поиска нужной информации в отсортированных массивах.
Предположим, что мы имеем некоторый отсортированный массив, и перед нами стоит задача: найти в этом массиве тот элемент, который находится ближе всего по значению к некоторому данному числу (далее будем называть его "X").
Первое, что приходит в голову - это перебрать все элементы массива и вычислить разницу между каждым из них и числом "X". Тот, у которого разница будет наименьшей по модулю, и будет являться ближайшим элементом массива к числу "X". Если в отсортированном массиве малое количество элементов (до 5-ти), то такой метод вполне подойдёт, но давайте подумаем, какое количество операций компьютер должен выполнить, если отсортированный массив состоит из 100 элементов. Нам потребуется выполнить почти столько же операций сравнения, сколько элементов в массиве находится перед искомым числом. Т.е., в самом худшем случае, когда искомый элемент массива находится в конце, нам потребуется выполнить сто операций сравнения. Это очень трудоёмкое занятие.
Можно ли как-то ускорить процесс поиска в от сортированном массиве? До сих пор мы не использовали тот факт, что массив отсортирован. Для ускорения поиска, предлагается использовать метод деления пополам - метод дихотомии.
Метод дихотомии заключается в следующем: выяснив, сколько всего элементов в отсортированном массиве, мы сравниваем число "X" со средним элементом массива. Если средний элемент массива больше, чем "X" - значит все элементы массива стоящие после среднего элемента массива тоже больше чем число "X", ведь мы работаем с отсортированным массивом. Следовательно, нам следует продолжить поиск в оставшейся части массива, расположенной до среднего элемента. Выяснив, сколько элементов в оставшейся части массива, мы опять выбираем средний элемент и сравниваем с ним число "X". Итак, для поиска нужного элемента остаётся только четверть массива. Затем границы поиска сужаются ещё больше - до восьмой части массива и так далее, до тех пор, пока не найдётся элемент массива равный числу "X" или пока не останутся два элемента массива, один больше числа "X", а другой меньше.
На рис. 1 видно, как сокращается пространство поиска нужного нам элемента. Искомый элемент обозначен красной меткой, середины оставшихся частей массива - зелёными метками, отбрасываемая часть массива - серым цветом.
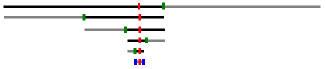
Для наглядности мы не стали наносить все элементы массива на отрезок, но если взглянуть на нижний отрезок и, учитывая, что он, в 32 раза меньший, чем исходный, содержит 2 элемента, становится понятно, что изначально мы имели массив приблизительно из 60 элементов. В результате применения метода дихотомии, выполнив всего лишь 6 операций сравнения, мы смогли закончить поиск. Если бы осуществлялся поиск прямым перебором, то нам потребовалось бы около 30 операций сравнения. Выигрыш на лицо.
Теперь попробуем реализовать этот метод поиска на MQL II. Нам потребуется несколько раз осуществлять похожие действия, значит, нам потребуется конструкция "цикл". Так как мы заранее не знаем о том, как долго нам придётся выполнять поиск, мы возьмём цикл "while". Остальное станет ясно из кода и комментариев к нему.
В следующей статье мы научимся на практике применять метод сортировки.
array: values[100](0);
//изначально левый край массива для
//поиска совпадает с началом массива values
var: left(0);
//изначально правый край массива для
//поиска совпадает с концом массива values
var: right(99);
//Средний элемент
var: middle(50);
//заполняем массив values числами Фибоначчи
var: ix(0);
values[0]=1;
values[1]=1;
for ix = 2 to 99 {
values[ix] = values[ix-1] + values[ix-2];
};
//будем искать среди чисел Фибонначи
//ближайшее к нашему"X"
var: X(123);
//переменная"found"будет содержать значение"false"
//до тех пор,пока мы не закончим поиск
var: found(false);
//продолжать искать до тех пор, пока переменная
// "found" не примет значение "true"
while is not found {
//вычисляем середину массива для поиска
//если (right - left)/2 не целое число, то
//его следует округлить до ближайшего целого
middle = left + round((right - left)/2);
//если середина находится правее нашего элемента
//и края массива для поиска ещё не стали двумя
//соседними элементами то...
if ((values[middle] > X) and (right - left > 1)) then {
// ...то меняем правый конец массива для поиска
// -им становится наша, теперь уже бывшая, середина
right = middle;
} else
//иначе если середина находится левее нашего элемента
//и края массива для поиска ещё не стали двумя
//соседними элементами то...
if ((values[middle] < X) and (right - left > 1)) then {
// ...то меняем левый конец массива для поиска
// -им становится наша, теперь уже бывшая,середина
left = middle;
} else if (values[middle] == X) then {
//иначе середина совпадает по значению с нашим элементом.
//это означает, что нам следует присвоить переменной
// found значение "true" и тем самым прекратить поиск,
//выйдя из цикла "while"
found = true;
} else {
//границы для поиска сузились настолько,
//что стали соседними элементами - это означает,
//что нам следует прекратить поиск, выйдя из цикла "while"
break;
};
};
//и тем не менее поиск ещё не завершён
if is found then {
//мы вышли из цикла "while" найдя элемент массива
//совпадающий по значению с искомым
print("Элемент с номером" + middle + "и значением" + values[middle] + "совпадает с искомым");
} else {
//мы вышли из цикла"while" из-за того, что
//границы для поиска сузились настолько, что
//стали соседними элементами - это означает,
//что нам следует ещё сравнить искомый элемент
//на предмет к какому из оставшихся элементов
//он ближе
if((values[right] - X) - (X - values[left]) > 0) then {
print("Элемент с номером" + left + "и значением" + values[left] + "ближе всех к искомому");
} else if((values[right] - X) - (X - values[left]) < 0) then {print("Элемент с номером" + right + "и значением" + values[right] + "ближе всех к искомому");
} else {print("Искомыое число находится ровно между элементом с номером" + left + "и значением" + values[left] + "и элементом с номером" + right + "и значением" + values[right]);
}
}
Александр Иванов (AKA HORN)
http://forex.tomsk.ru
Материал предоставлен : http://www.forextimes.ru/magazine
Cтатья опубликована на сайте "Форекс форум. Торговля на Forex. Cообщество трейдеров":
http://youfx.ru
Адрес статьи:
http://youfx.ru/modules/myarticles/article_storyid_8.html |

